Explaining Their Thinking
Overview
When students explain their thinking process aloud with guidance in response to questions or prompts, they recognize the strategies they use and solidify their understanding. Think-alouds, sometimes called reflective questioning, require students to reflect on the details of a problem, the steps needed to solve it, and the mathematical reasoning behind those decisions. They can also be used as formative assessment to monitor students' understanding and address any misconceptions. Research cautions that this strategy is most effective when students are prompted with specific protocols or questions, and that prompts should be carefully aligned with target learning outcomes so students avoid reinforcing incorrect approaches or choices.
Example: Use This Strategy in the Classroom
Watch how this teacher models using a think-aloud to solve an algebraic problem. As she verbalizes her thinking, she incorporates mathematical vocabulary while walking through her problem-solving process.
Design It into Your Product
Videos are chosen as examples of strategies in action. These choices are not endorsements of the products or evidence of use of research to develop the feature.
Starting at 1:26, learn how digital portfolios like Seesaw allow students to take photos of their math work and voice record their thinking.
Additional Resources
Additional examples, research, and professional development. These resources are possible representations of this strategy, not endorsements.
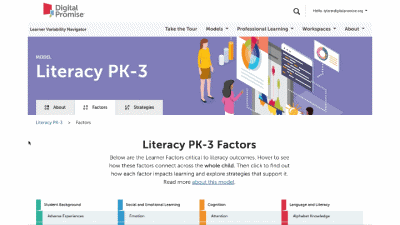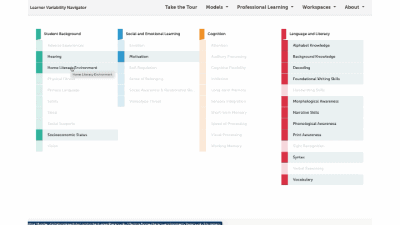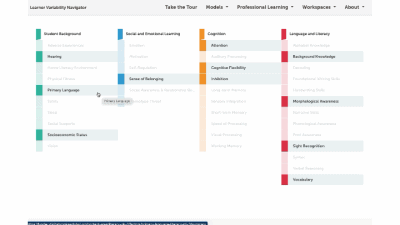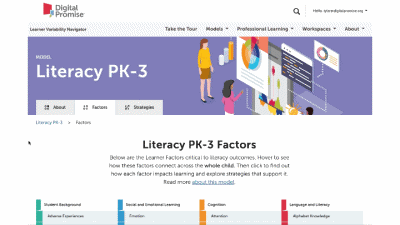
Factors Supported by this Strategy
More Active Learning Strategies
Students activate more cognitive processes by exploring and representing their understandings in visual form.
Analyzing incorrect worked examples is especially beneficial for helping students develop a conceptual understanding of mathematical processes.
Math games allow students to practice many math skills in a fun, applied context.
Project-based learning (PBL) actively engages learners in authentic tasks designed to create products that answer a given question or solve a problem.
Response devices boost engagement by encouraging all students to answer every question.
When students create their own number and word problems, they connect math concepts to their background knowledge and lived experiences.
Analyzing and discussing solved problems helps students develop a deeper understanding of abstract mathematical processes.
