Given the robust nature of learning sciences research, this website is best viewed on tablets and computers. A small screen experience is coming in the future.
On June 22, 2021, we will launch updated strategies for the Math PK-2 model, as well as additional updates to the Navigator that highlight equity, SEL, and culturally responsive teaching. To learn more, visit our Site Updates (available in the "About" menu at the top of any page).
Hover to see how factors connect to Proportional Reasoning. Then click connected factors to explore strategies related to multiple factors.
Proportional Reasoning involves an understanding of ratio and the relationships between ratios. Ratios express a part-to-whole relationship that can be represented in the form of fractions, percentages, or rates. Proportional Reasoning is an essential component of arithmetic proficiency in elementary school and provides entry to higher math skills including algebra, geometry, and probability and statistics.
Students begin with an informal understanding of proportional relationships (e.g., partitioning or fair sharing, or relating proportions in shaded areas of shapes). This informal knowledge develops over several years into a more formal conceptual understanding as they connect different aspects of Proportional Reasoning including:
While Proportional Reasoning is challenging for many students in the early years, those students with dyscalculia often demonstrate persistent difficulties that do not resolve without intervention.
Students activate more cognitive processes by exploring and representing their understandings in visual form.
Analyzing incorrect worked examples is especially beneficial for helping students develop a conceptual understanding of mathematical processes.
Project-based learning (PBL) actively engages learners in authentic tasks designed to create products that answer a given question or solve a problem.
Math games allow students to practice many math skills in a fun, applied context.
When students create their own number and word problems, they connect math concepts to their background knowledge and lived experiences.
Analyzing and discussing solved problems helps students develop a deeper understanding of abstract mathematical processes.
Flexible grouping is a classroom practice that temporarily places students together in given groups to work together, with the purpose of achieving a given learning goal or activity.
Having students teach their knowledge, skills, and understanding to their classmates strengthens learning.
Rhyming, alliteration, and other sound devices reinforce math skills development by activating the mental processes that promote memory.
Easy access to seeing the relationships between numbers promotes Number Sense as students see these connections repeatedly.
Providing math tasks with high cognitive demand conveys high expectations for all students by challenging them to engage in higher-order thinking.
CRA is a sequential instructional approach during which students move from working with concrete materials to creating representational drawings to using abstract symbols.
Knowing the language of math is critical because students must use this language to understand math concepts and determine calculations needed.
Thinking of and about patterns encourages learners to look for and understand the rules and relationships that are critical components of mathematical reasoning.
Discussing strategies for solving mathematics problems after initially letting students attempt to problem solve on their own helps them understand how to organize their mathematical thinking and intentionally tackle problems.
Teaching students to recognize common problem structures helps them transfer solution methods from familiar to unfamiliar problems.
In guided inquiry, teachers help students use their own language for constructing knowledge by active listening and questioning.
Math centers support learner interests and promote the development of more complex math skills and social interactions.
When teachers connect math to the students' world, students see how math is relevant and applicable to their daily lives.
A strengths-based approach is one where educators intentionally identify, communicate, and harness students' assets, across many aspects of the whole child, in order to empower them to flourish.
Writing that encourages students to articulate their understanding of math concepts or explain math ideas helps deepen students' mathematical understanding.
Adding motions to complement learning activates more cognitive processes for recall and understanding.
Providing physical and virtual representations of numbers and math concepts helps activate mental processes.
Connecting information to music and dance can support Short-term and Long-term Memory by engaging auditory processes, Emotions, and physical activity.
Math games and manipulatives for vision differences support math development for learners with visual needs.
Children's literature can be a welcoming way to help students learn math vocabulary and concepts.
Continual use of foundational skills with different problems reinforces a conceptual understanding of math skills.
Daily review strengthens previous learning and can lead to fluent recall.
Spending time with new content helps move concepts and ideas into Long-term Memory.
By talking through their thinking at each step of a process, teachers can model what learning looks like.
Visualizing how ideas fit together helps students construct meaning and strengthens recall.
Visual representations help students understand what a number represents as well as recognize relationships between numbers.
Learning about students' cultures and connecting them to instructional practices helps foster a sense of belonging and mitigate Stereotype Threat.
Translanguaging is a flexible classroom practice enabling students to listen, speak, read, and write across their multiple languages or dialects, even if the teacher does not have formal knowledge of these additional languages.
Except where otherwise noted, content on this site is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License
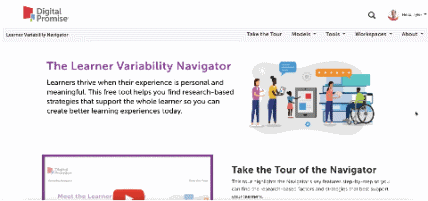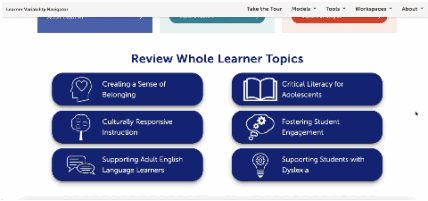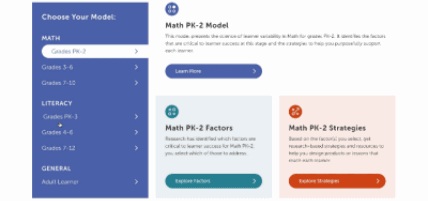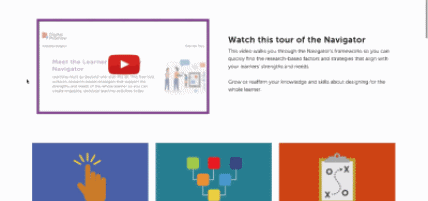
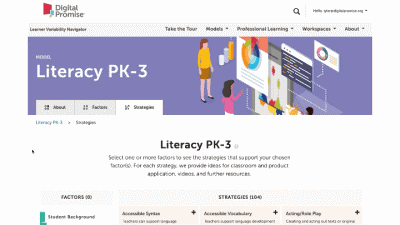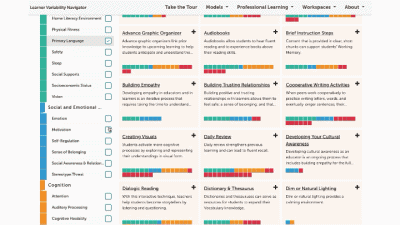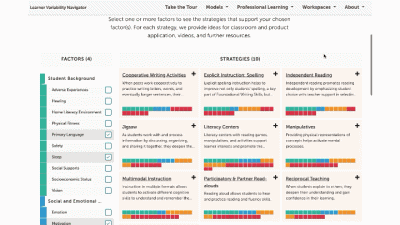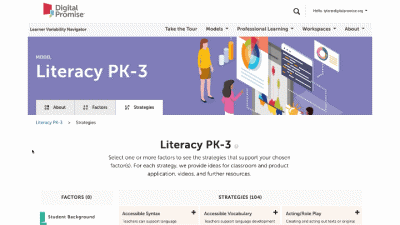
This is our homepage. You can access many of the features of the Navigator here, and learn more about how learner variability intersects with topics in education and learning. To start, select a content area – we call them Learner Models – to visit a factor map.
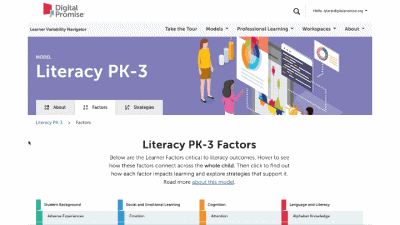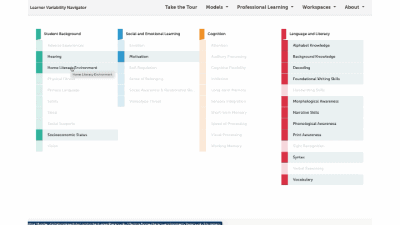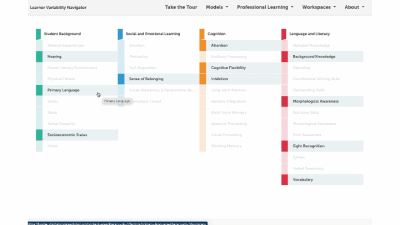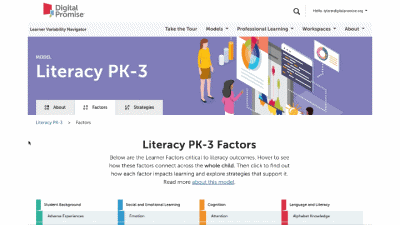
Factor maps show research-based concepts, "factors," that likely impact learning. They are organized into four categories: Learner Background, Social and Emotional Learning, Cognition, and Content Area. The map is interactive. Move your cursor over a factor to see connected factors. Select any factor to visit its summary page. We'll look at factor summary pages next.
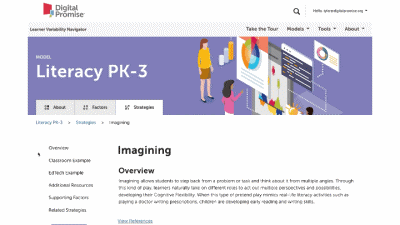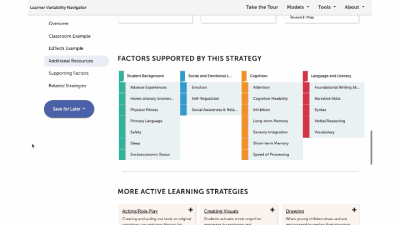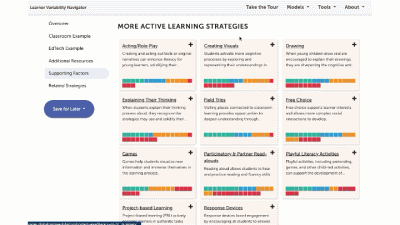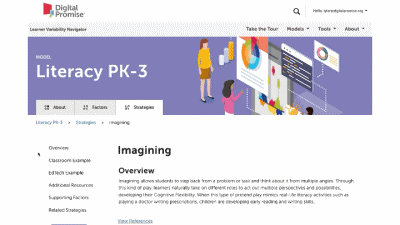
This is a factor summary page. It provides a brief definition and review of the factor, a factor connections diagram, additional resources, and strategies that support this factor. On the strategy card, the multi-colored boxes show all the factors that it supports. Select a strategy to visit its summary page.
Strategy summary pages have an overview, information about using the strategy in different learning environments, resources of interest, the factors this strategy supports, and related strategies you can explore. To view all the strategies in a content area, use the strategies tab at the top of the page. We'll look at all the Strategies for this learner model next.
The strategy page shows ALL of the strategies for that learner model. You can select factors of interest for you or your learners, and it will narrow the strategies to only those that match all of the factors selected. This makes it easy to find key strategies to better design for learner variability. Again, select the strategy name to visit its summary page.
Already a user? LOG IN
Are you sure you want to delete this Workspace?
Enter the email address of the person you want to share with. This person will be granted access to this workspace and will be able to view and edit it.
Adjust the permissions of your Workspace.
This Workspace is .
This Workspace's Reflection Area is .
Learner variability is the recognition that each learner is a unique constellation of strengths and challenges that are interconnected across the whole child. Understanding these connections and how they vary according to context is essential for meeting the needs of each learner.
It disrupts the notion of a one-size-fits all education. Understanding learner variability helps educators embrace both students’ struggles and strengths as we connect practice to uplifting the whole learner.
Throughout the site, we talk about "factors" and "strategies." Factors are concepts research suggests have an impact on how people learn. Strategies are the approaches to teaching and learning that can be used to support people in how they learn best.
Use the Learner Centered Design Tool to build a workspace. Go to Learner Centered Design Tool.
Or, create a new blank workspace for your product or project.
Use one of the guided tools to build a workspace.
Or, create a new blank workspace for your product or project.
Make a copy of this workspace.
Redirecting soon...
Generating summary page
Loading...
On this page, using your heatmap, you will be asked to select factors to further explore, and then select new strategies you might incorporate into upcoming instruction. Once done, click “Show Summary" to view your Design Summary Report.
On this page, using your heatmap, you will be asked to select factors to further explore, and then select new strategies you might incorporate into upcoming instruction. Once done, click “Show Report” to view your Design Summary Report.
By selecting "Show Report" you will be taken to the Assessment Summary Page. Once created, you will not be able to edit your report. If you select cancel below, you can continue to edit your factor and strategy selections.
Announcement here
Item successfully added to workspace!
Issue adding item to workspace. Please refresh the page and try again.
Learner variability is the recognition that each learner is a unique constellation of strengths and challenges that are interconnected across the whole child. Understanding these connections and how they vary according to context is essential for meeting the needs of each learner. It embraces both students’ struggles and strengths. It considers the whole child.
Throughout the site, we talk about "factors" and "strategies." Factors are concepts research suggests have an impact on how people learn. Strategies are the approaches to teaching and learning that can be used to support people in how they learn best.
The Learner Variability Navigator is a free, online tool that translates the science of learner variability into factor maps and strategies that highlight connections across the whole learner. This puts the science of learning at teachers' fingertips, empowering them to understand their own practice and support each learner.
