Peer Teaching
Overview
Having students teach their knowledge, skills, and understanding to their classmates strengthens learning. Preparing to teach and then explaining a concept in their own words improves students' clarity of understanding and Math Communication skills, as well as supports greater retention in Long-term Memory.
Example: Use This Strategy in the Classroom
Watch how these students check on each others' understanding when solving order of operation problems. Throughout the activity, students provide feedback and correction. Explaining concepts in their own words can improve students' clarity of understanding as well as support Long-term Memory.
Design It into Your Product
Additional Resources
Additional examples, research, and professional development. These resources are possible representations of this strategy, not endorsements.
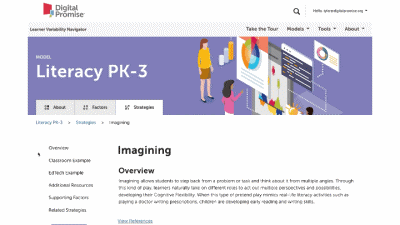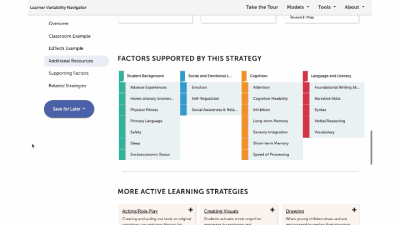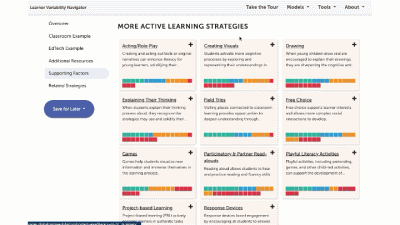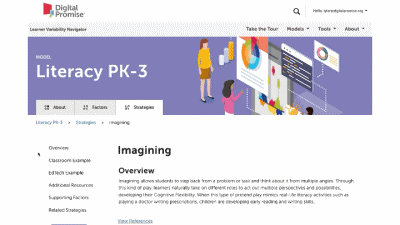
Factors Supported by this Strategy
More Cooperative Learning Strategies
As students solve problems in a group, they learn new strategies and practice communicating their mathematical thinking.
Flexible grouping is a classroom practice that temporarily places students together in given groups to work together, with the purpose of achieving a given learning goal or activity.
As students walk through stations working in small groups, the social and physical nature of the learning supports deeper understanding.
As students work with and process information by discussing, organizing, and sharing it together, they deepen their understanding.
When students have meaningful conversations about math and use math vocabulary, they develop the thinking, questioning, and explanation skills needed to master mathematical concepts.
Students deepen their understanding and gain confidence in their learning when they explain to and receive feedback from others.
Respectful redirection, or error correction, outlines a clear and concise way that educators can provide feedback on behaviors that need immediate correction, in a positive manner.
Students deepen their math understanding as they use and hear others use specific math language in informal ways.
