Given the robust nature of learning sciences research, this website is best viewed on tablets and computers. A small screen experience is coming in the future.
On June 22, 2021, we will launch updated strategies for the Math PK-2 model, as well as additional updates to the Navigator that highlight equity, SEL, and culturally responsive teaching. To learn more, visit our Site Updates (available in the "About" menu at the top of any page).
Hover to see how factors connect to Short-term Memory. Then click connected factors to explore strategies related to multiple factors.
Short-term Memory stores a limited amount of information for up to 30 seconds. It is our holding tank for skills and knowledge that, with practice, will move to Long-term Memory. The amount of information that can be stored in Short-term Memory capacity increases significantly during childhood and into adolescence. Students' Short-term Memory capacity, particularly the visuospatial component, is related to their improved math performance.
There are two types of Short-term Memory:
Short-term Memory is different from Working Memory because information is not manipulated in Short-term Memory, as it is in Working Memory. When items in Short-term Memory are rehearsed sufficiently, they are consolidated to become part of Long-term Memory.
Teachers support language development by using and providing vocabulary and syntax that is appropriately leveled (e.g., using simple sentences when introducing complex concepts).
Content that is provided in clear, short chunks can support students' Working Memory.
Providing math tasks with high cognitive demand conveys high expectations for all students by challenging them to engage in higher-order thinking.
As students solve problems in a group, they learn new strategies and practice communicating their mathematical thinking.
Communication boards are displays of graphics (e.g., pictures, symbols, illustrations) and/or words where learners can gesture or point to the displays to extend their expressive language potential.
CRA is a sequential instructional approach during which students move from working with concrete materials to creating representational drawings to using abstract symbols.
Students activate more cognitive processes by exploring and representing their understandings in visual form.
Continual use of foundational skills with different problems reinforces a conceptual understanding of math skills.
10 minutes in each math session devoted to building fluent retrieval of basic math facts sets the foundation for learning new concepts.
Daily review strengthens previous learning and can lead to fluent recall.
Knowing the language of math is critical because students must use this language to understand math concepts and determine calculations needed.
Thinking of and about patterns encourages learners to look for and understand the rules and relationships that are critical components of mathematical reasoning.
Teaching students to recognize common problem structures helps them transfer solution methods from familiar to unfamiliar problems.
Discussing strategies for solving mathematics problems after initially letting students attempt to problem solve on their own helps them understand how to organize their mathematical thinking and intentionally tackle problems.
Analyzing incorrect worked examples is especially beneficial for helping students develop a conceptual understanding of mathematical processes.
When students explain their thinking process aloud with guidance in response to questions or prompts, they recognize the strategies they use and solidify their understanding.
Teachers can help students understand that learning involves effort, mistakes, and reflection by teaching them about their malleable brain and modeling their own learning process.
As students walk through stations working in small groups, the social and physical nature of the learning supports deeper understanding.
Adding motions to complement learning activates more cognitive processes for recall and understanding.
In guided inquiry, teachers help students use their own language for constructing knowledge by active listening and questioning.
Spending time with new content helps move concepts and ideas into Long-term Memory.
Practicing until achieving several error-free attempts is critical for retention.
As students work with and process information by discussing, organizing, and sharing it together, they deepen their understanding.
Math centers support learner interests and promote the development of more complex math skills and social interactions.
Math games allow students to practice many math skills in a fun, applied context.
Rhyming, alliteration, and other sound devices reinforce math skills development by activating the mental processes that promote memory.
When students have meaningful conversations about math and use math vocabulary, they develop the thinking, questioning, and explanation skills needed to master mathematical concepts.
A mnemonic device is a creative way to support memory for new information using connections to current knowledge, for example by creating visuals, acronyms, or rhymes.
By talking through their thinking at each step of a process, teachers can model what learning looks like.
Teachers sharing math-to-self, math-to-math, and math-to-world connections models this schema building.
Brain breaks that include movement allow learners to refresh their thinking and focus on learning new information.
Instruction in multiple formats allows students to activate different cognitive skills to understand and remember the steps they are to take in their math work.
Multiple display spaces help develop oral language skills as well as Social Awareness & Relationship Skills by allowing groups to share information easily as they work.
Visualizing how ideas fit together helps students construct meaning and strengthens recall.
Providing physical and virtual representations of numbers and math concepts helps activate mental processes.
Easy access to seeing the relationships between numbers promotes Number Sense as students see these connections repeatedly.
Visual representations help students understand what a number represents as well as recognize relationships between numbers.
Multiple writing surfaces promote collaboration by allowing groups to share information easily as they work.
Connecting information to music and dance can support Short-term and Long-term Memory by engaging auditory processes, Emotions, and physical activity.
Having students teach their knowledge, skills, and understanding to their classmates strengthens learning.
Research shows physical activity improves focus and creativity.
Decreasing extra audio input provides a focused learning environment.
When teachers connect math to the students' world, students see how math is relevant and applicable to their daily lives.
Students deepen their understanding and gain confidence in their learning when they explain to and receive feedback from others.
Response devices boost engagement by encouraging all students to answer every question.
When students engage in a dialogue with themselves, they are able to orient, organize, and focus their thinking.
When students monitor their comprehension, behavior, or use of strategies, they build their Metacognition.
Sentence frames or stems can serve as language support to enrich students' participation in academic discussions.
When students create their own number and word problems, they connect math concepts to their background knowledge and lived experiences.
Transforming written text into audio activates different parts of the brain to support learning.
Students deepen their math understanding as they use and hear others use specific math language in informal ways.
Tossing a ball, beanbag, dice, or other small object activates physical focus in support of mental focus.
Having students verbally repeat information such as instructions ensures they have heard and supports remembering.
Providing visuals to introduce, support, or review instruction activates more cognitive processes to support learning.
Visual supports, like text magnification, colored overlays, and guided reading strip, help students focus and properly track as they read.
Wait time, or think time, of three or more seconds after posing a question increases how many students volunteer and the length and accuracy of their responses.
A word wall helps build the Math Communication and vocabulary skills that are necessary for problem solving.
Analyzing and discussing solved problems helps students develop a deeper understanding of abstract mathematical processes.
Writing that encourages students to articulate their understanding of math concepts or explain math ideas helps deepen students' mathematical understanding.
Except where otherwise noted, content on this site is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License
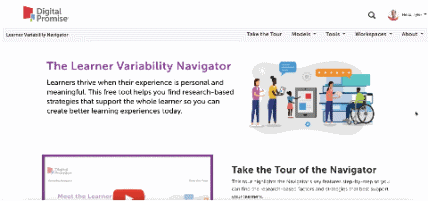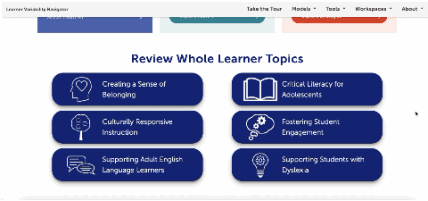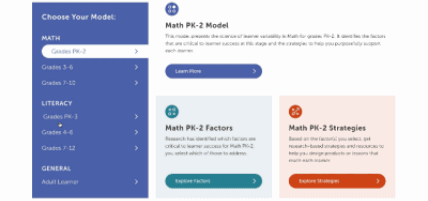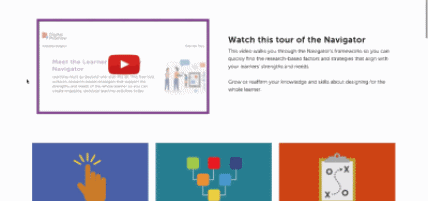
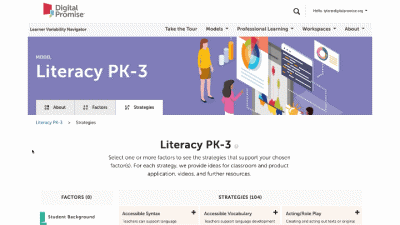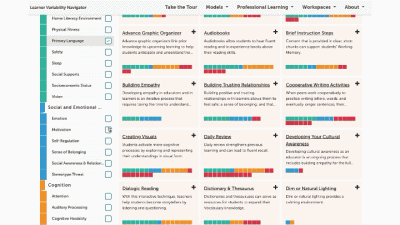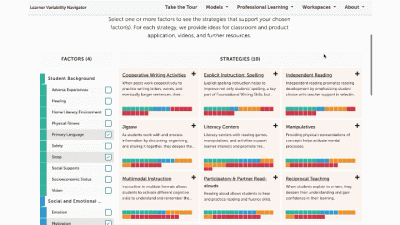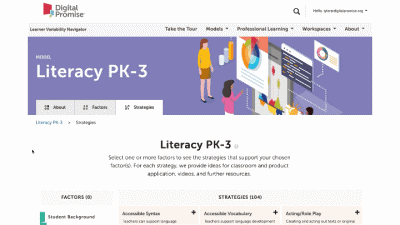
This is our homepage. You can access many of the features of the Navigator here, and learn more about how learner variability intersects with topics in education and learning. To start, select a content area – we call them Learner Models – to visit a factor map.
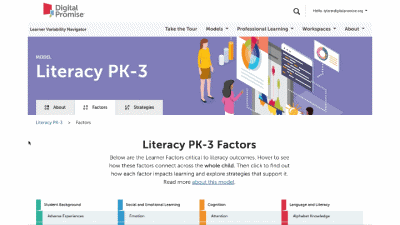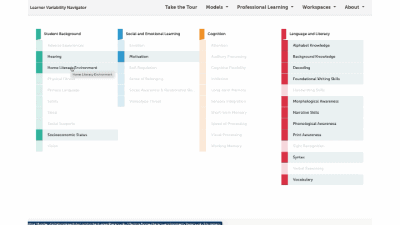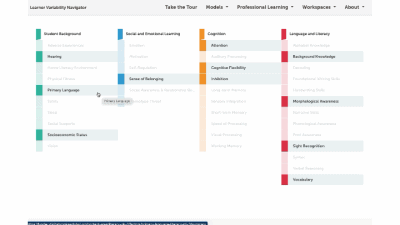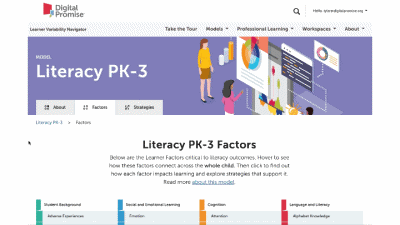
Factor maps show research-based concepts, "factors," that likely impact learning. They are organized into four categories: Learner Background, Social and Emotional Learning, Cognition, and Content Area. The map is interactive. Move your cursor over a factor to see connected factors. Select any factor to visit its summary page. We'll look at factor summary pages next.
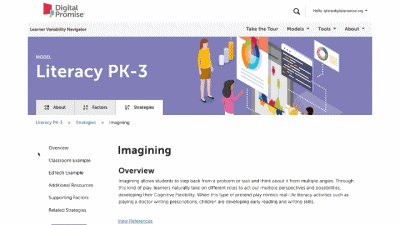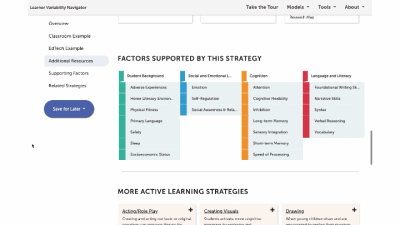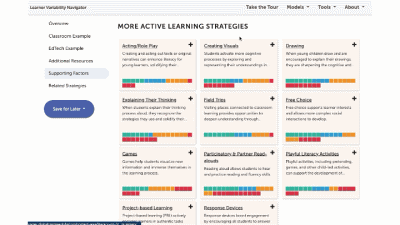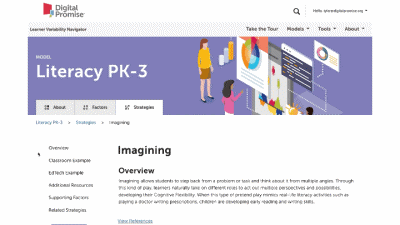
This is a factor summary page. It provides a brief definition and review of the factor, a factor connections diagram, additional resources, and strategies that support this factor. On the strategy card, the multi-colored boxes show all the factors that it supports. Select a strategy to visit its summary page.
Strategy summary pages have an overview, information about using the strategy in different learning environments, resources of interest, the factors this strategy supports, and related strategies you can explore. To view all the strategies in a content area, use the strategies tab at the top of the page. We'll look at all the Strategies for this learner model next.
The strategy page shows ALL of the strategies for that learner model. You can select factors of interest for you or your learners, and it will narrow the strategies to only those that match all of the factors selected. This makes it easy to find key strategies to better design for learner variability. Again, select the strategy name to visit its summary page. Use the plus signs on each strategy card to add a strategy to a workspace. We'll explore those next.
The “Tools & Workspaces” tab on the navigation bar or the “My Workspaces” button on the account menu takes you to a page that shows your workspaces. There are two tabs on the My Workspaces page: a Workspaces tab and a Reports tab. The Workspaces tab lists workspaces you can personalize and update. You can create new sections, move cards between sections, add annotations, share with collaborators, and write reflections. The second tab, "Reports", are a kind of workspace created through the Instructional Design Tool or the Product Assessment Tool and have fewer personalization options.
There are three, step-by-step tools you can access on the Navigator to help make workspace or a workspace report. The Learner Centered Design Tool has four steps and helps you create a workspace. First, enter basic information and select a content area of interest. Second, select a few factors that you want to focus on. Third, review connected factors you may not have considered. Note – you don't have to select any extra factors on this step if you don’t want to. The fourth and final step, review and select strategies that you want to use, and save them to a workspace.
Already a user? LOG IN
Are you sure you want to delete this Workspace?
Enter the email address of the person you want to share with. This person will be granted access to this workspace and will be able to view and edit it.
Adjust the permissions of your Workspace.
This Workspace is .
This Workspace's Reflection Area is .
Learner variability is the recognition that each learner is a unique constellation of strengths and challenges that are interconnected across the whole child. Understanding these connections and how they vary according to context is essential for meeting the needs of each learner.
It disrupts the notion of a one-size-fits all education. Understanding learner variability helps educators embrace both students’ struggles and strengths as we connect practice to uplifting the whole learner.
Throughout the site, we talk about "factors" and "strategies." Factors are concepts research suggests have an impact on how people learn. Strategies are the approaches to teaching and learning that can be used to support people in how they learn best.
Use the Learner Centered Design Tool to build a workspace. Go to Learner Centered Design Tool.
Or, create a new blank workspace for your product or project.
Use one of the guided tools to build a workspace.
Or, create a new blank workspace for your product or project.
Make a copy of this workspace.
Redirecting soon...
Generating summary page
Loading...
On this page, using your heatmap, you will be asked to select factors to further explore, and then select new strategies you might incorporate into upcoming instruction. Once done, click “Show Summary" to view your Design Summary Report.
On this page, using your heatmap, you will be asked to select factors to further explore, and then select new strategies you might incorporate into upcoming instruction. Once done, click “Show Report” to view your Design Summary Report.
By selecting "Show Report" you will be taken to the Assessment Summary Page. Once created, you will not be able to edit your report. If you select cancel below, you can continue to edit your factor and strategy selections.
Announcement here
Item successfully added to workspace!
Issue adding item to workspace. Please refresh the page and try again.
Learner variability is the recognition that each learner is a unique constellation of strengths and challenges that are interconnected across the whole child. Understanding these connections and how they vary according to context is essential for meeting the needs of each learner. It embraces both students’ struggles and strengths. It considers the whole child.
Throughout the site, we talk about "factors" and "strategies." Factors are concepts research suggests have an impact on how people learn. Strategies are the approaches to teaching and learning that can be used to support people in how they learn best.
The Learner Variability Navigator is a free, online tool that translates the science of learner variability into factor maps and strategies that highlight connections across the whole learner. This puts the science of learning at teachers' fingertips, empowering them to understand their own practice and support each learner.
