Culturally Responsive Math Teaching: Mathematical Thinking
This workspace focuses on equity and includes some of the key factors and strategies that can contribute to and promote a culturally responsive mathematics classroom. This workspace focuses on 3 dimensions of mathematical thinking: math knowledge, cognitive demand and math communication/discourse (Aguirre & Zavala, 2013).
STRATEGIES THAT SUPPORT cognitive demand
Math PK-2
In guided inquiry, teachers help students use their own language for constructing knowledge by active listening and questioning.
Math PK-2
Three-phase lesson format is a problem-solving structure to promote meaningful math learning by activating prior knowledge, letting students explore mathematical thinking, and promoting a math community of learners.
Math PK-2
Students activate more cognitive processes by exploring and representing their understandings in visual form.
Math 3-6
Providing math tasks with high cognitive demand conveys high expectations for all students by challenging them to engage in higher-order thinking.
Math 3-6
In guided inquiry, teachers help students use their own language for constructing knowledge by active listening and questioning.
Math 3-6
When students explain their thinking process aloud with guidance in response to questions or prompts, they recognize the strategies they use and solidify their understanding.
Math 7-10
Students activate more cognitive processes by exploring and representing their understandings in visual form.
Math 7-10
Analyzing and discussing solved problems helps students develop a deeper understanding of abstract mathematical processes.
Math 7-10
CRA is a sequential instructional approach during which students move from working with concrete materials to creating representational drawings to using abstract symbols.
STRATEGIES THAT SUPPORT math communication & Discourse
Math PK-2
When students explain their thinking process aloud with guidance in response to questions or prompts, they recognize the strategies they use and solidify their understanding.
Math PK-2
A word wall helps build the mathematical vocabulary and Language Skills that are necessary for problem solving.
Math 3-6
Analyzing incorrect worked examples is especially beneficial for helping students develop a conceptual understanding of mathematical processes.
Math 3-6
Writing that encourages students to articulate their understanding of math concepts or explain math ideas helps deepen students' mathematical understanding.
Math 3-6
As students walk through stations working in small groups, the social and physical nature of the learning supports deeper understanding.
Math 7-10
Having students teach their knowledge, skills, and understanding to their classmates strengthens learning.
Math 7-10
When students have meaningful discussions about math and use math vocabulary, they develop the thinking, questioning, and explanation skills needed to master mathematical concepts.
Math 7-10
The flipped classroom has two parts: cooperative group activities in class and digitally-based individual instruction out of class.
Math PK-2
As students solve problems in a group, they learn new strategies and practice communicating their mathematical thinking.
strategies that support math knowledge & understanding
Math PK-2
Providing physical representations of numbers and math concepts helps activate mental processes.
Math PK-2
Easy access to seeing the relationships between numbers promotes number sense as students see these connections repeatedly.
Math 3-6
Visual representations help students understand what a number represents as well as recognize relationships between numbers.
Math 3-6
Providing physical and virtual representations of numbers and math concepts helps activate mental processes.
Math 7-10
When teachers connect math to the students' world, students see how math is relevant and applicable to their daily lives.
Math 7-10
Providing physical and virtual representations of numbers and math concepts helps activate mental processes.
Math 7-10
Visual representations help students understand what a number represents as well as recognize relationships between numbers.
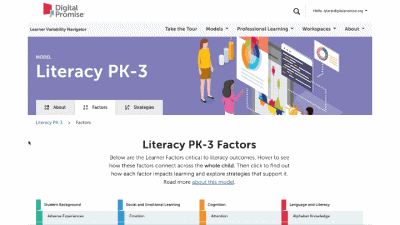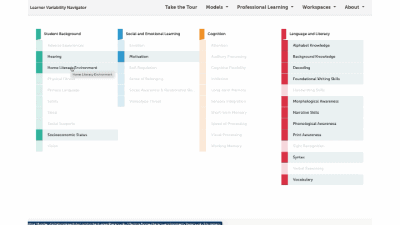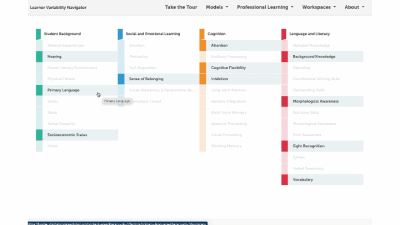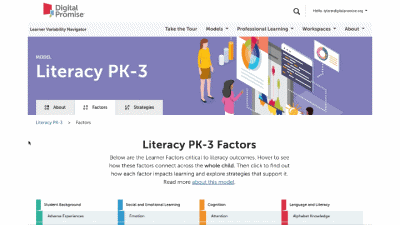
FACTORS RELATED TO MATHematical thinking
Arithmetic Fact Retrieval requires efficiently, accurately, and flexibly drawing basic number combinations from Long-term Memory to use in performing more complex calculations.
Cognitive Flexibility, a component of executive functioning, is the ability to effectively adapt our behavior as we face changing environmental and task demands.
Mathematical Flexibility is the ability to maintain and flexibly shift among multiple representations of numbers and problem-solving strategies.
Visual Processing is seeing at the cognitive level: taking the input that comes through our Vision and working to understand what we see.
Working Memory, a component of executive functioning, allows a person to temporarily hold and manipulate information to apply in other processes.
Many of the Language Skills that are critical for reading are also important for math success.
Algebraic Thinking is the ability to generalize, represent, justify, and reason with abstract mathematical structures and relationships.
Reasoning is the ability to think abstractly, draw inferences, identify patterns and relationships, and apply logic in order to flexibly solve novel problems.
Mathematical Flexibility is the ability to maintain and shift among multiple representations of numbers and between problem-solving strategies in an adaptive manner.
Language and literacy skills support many aspects of math problem solving.
Students typically begin by thinking about Operations as telling them which procedural calculations, or computations, to do (such as finding the sum or difference of two numbers).
Visual Processing is seeing at the cognitive level: taking the input that comes through our Vision and working to understand what we see.
Algebraic Thinking is the ability to generalize, represent, justify, and reason with abstract mathematical structures and relationships.
Geometric Reasoning involves using abstract thinking to define, analyze, and make arguments about shapes and spatial relationships.
Proportional Reasoning involves an understanding of ratio and the relationships between ratios.
Language and literacy skills support many aspects of math problem solving.
Statistical Reasoning involves thinking about and understanding uncertainty and building mental models to capture key aspects of real world phenomena.
Reasoning is the ability to think abstractly, draw inferences, identify patterns and relationships, and apply logic in order to flexibly solve novel problems.
Visual Processing is seeing at the cognitive level: taking the input that comes through our Vision and working to understand what we see.
While the executive functions Inhibition and Working Memory are very much related processes and show similar developmental trajectories in childhood, they become more distinct processes during adolescence.